摘录自网络：

背景知识

正弦函数和其所对应的正弦波估计是信号处理中最重要最常用的工具。

全都可用如下式子表示: $f(t)=c_0+\sum_{1}^\infty c_ncos(n\omega t+\psi) \tag{1.1}$

正弦波主要有如下几个概念：波幅、频率（角速度）、相位 $f(n)=Asin(\omega t+\psi)+k \tag{1.2}$ 其中$A$表示振幅，A越大，振幅越大。

$\omega$表示角速度，当然角速度和频率$f$ 是对应关系，信号处理中也常常用频率这种俗语来描述。

$\psi$表示相位，sin和cos两个正弦函数的差别其实也仅仅是相位不同

$k$是这个正弦波的偏移，可以理解为这个波在y轴上如何上下移动，这个会被统一分配到直流分量中（频率为0的波的波幅）。

由此可以知道信号是由哪些频率的正弦波构成，了解对应频率的波在信号中的能量和相位信息。

傅里叶变换

如何将$f(t)$分解为 $c_1co(\omega t+\psi)+c_2cos(2\omega t+\psi)+c_3cos(3\omega t+\psi)+\cdots \tag{2.1}$ 实际上傅里叶变换需要解决的就是这一点，它的最终目的就是要将信号分解为上面的形式，好让我们把不同频率的正弦波信号剥离出来。

• 1首先是频率

#一个重要结论：不同频率的正弦波相乘，对其周期积分后，其结果都是0！（信号变换中的公式都是以柯西主值积分为钦定的积分方式（整个无穷区间取周期倍），对于和差化积之后结果进行分析可知。）

这个概念我们又叫作波的相干性，比如给一段信号，问你信号里有没有100Hz频率的正弦波信号，可以把这个信号和100Hz的正弦波信号相乘，然后对其周期内积分，如果结果不是0，那么这个信号就含有100Hz的信号。

• 2对应幅度和相位

求该频率正弦波对应的幅度和相位，实际上就是求式1.1的$c_n$和$\psi$。

利用三角函数的变换公式，式(1.2)可变形为 $f(t)=c_0+\sum_{n=1}^{\infty}[c_ncos\psi cos(n\omega t)-c_nsin\psi sin(n\omega t)] \tag{2.2}$ 设$a_n=c_ncos\psi$，$b_n=-c_nsin\psi$，那么上式变为 $f(t)=c_0+\sum_{n=1}^{\infty}[a_ncos(n\omega t)+b_nsin(n\omega t)] \tag{2.3}$ 引入正交性，检波手段：假设我们对$f(t)$用$sin(k\omega t)$进行检波（即乘起来，方便计算其一个周期内积分），即有 $\int_0^{T}f(t)sin(k\omega t)dt \tag{2.4}$ 假设$f(x)$中含有$n\omega$角频率的正弦波系数为$b_n$，那么根据三角函数的正交性，别的频率的波积分后全变为0，只剩下$k=n$ 频率一样的情况，上式就有 $\int_0^{T}f(t)sin(n\omega t)dt=b_n\int_0^{T}sin(n\omega t)sin(k\omega t)dt=b_n\int_0^{T}sin(n\omega t)^2 dt \tag{2.5}$ 进一步计算，可得 $\int_0^Tf(t)sin(n\omega t)dt=b_{n}\frac{T}{2} \tag{2.6}$ 同理$a_n$也可以使用相同的方式进行推导。

因此，通过$a_nb_n$ 我们可以知道这个波的波幅与相位： $c_n=\sqrt{a_{n}^2+b_{n}^2} \tag{2.7}$

$$\psi=arctan(-\frac{b_n}{a_n}) \tag{2.8}$$

这就基本就是傅里叶变换中最核心的级数了

对比傅里叶变换的标准公式 $F(f(t))=\int_{-\infty}^{infty}f(t)e^{-i\omega t}dt \tag{2.9}$ 根据欧拉公式 $e^{i\theta}=cos(\theta)+isin(\theta) \tag{2.10}$ 把欧拉公式带入傅里叶变换得 $F(f(t))=\int_{-\infty}^{\infty}f(t)[cos(\omega t)-isin(\omega t)]dt \tag{2.11}$ 即 $F(f(t))=\int_{-\infty}^{\infty}f(t)cos(\omega t)dt-\int_{-\infty}^{\infty}f(t)isin(\omega t)dt \tag{2.12}$ 将式（2.11）与式（2.2）相比，可知多了一个复数，这个复数没有特别的意义，作用就是在计算中和cos区分开来。

拉普拉斯变换

首先看拉普拉斯变换公式 $F(s)=\int_{-\infty}^{\infty}f(t)e^{-st}dt=\int_{-\infty}^{\infty}f(t)e^{-(\sigma+i\omega)t}dt \tag{3.1}$ 与傅里叶公式对比可以发现即是傅里叶公式乘以一个$e^{-\sigma}$。为何如此，通过下图

这个信号的毛病在于,他已经上天了,是的,它增长的速度太快了,而我们却要使用不能够”上天”的正弦函数去拟合它,、傅里叶变换无法制造一个同样上天的正弦信号来拟合,我们就把它原本的信号”掰弯”,那么如何”掰弯”呢,简单,乘以一个$e^{-\sigma}$就行了。

拉普拉斯变换的意义无非就是把那些想要上天的函数掰弯,好最终变成那种适合做变换的函数,但是掰弯听起来不太专业,所以我们又管$e^{-\sigma}$叫衰减因子。

Z变换

信号是连续的,而计算机上存储的数据是离散的,这可咋办好。我们可以这样,每隔一小段距离,取一个点,最后用的时候把这些点连起来,不就能变成原来的的信号了么,当然我们还得研究研究,这个一小段距离究竟得多小,才不至于让原信号失真，这个就得参考香农采样定律了。

好的,现在我们把连续的信号换一下,换成离散的”点”,首先积分是不能用了,既然换成离散的了,积分对应的就应该变成累加符号$\sum$ ,当然$f(t)$也是不能用了,这是一个连续信号的写法,而离散的一个一个的点得换成 $x[n]$ ,其中的n表示第n个点,实际上就是时间变来的,当然$e^{-j\omega t}$也不能用了,你想啊,我们要具体到某个点,这个点怎么表示,当然了,首先把时间$t$换成$n$索引号,然后$\omega$这个动态的角速度值换成具体的角度$\psi$。

好了,我们终于把连续信号的傅里叶变换变成了离散信号的傅里叶变换,写写看 $A\sum_{-\infty}^{\infty}x[n]e^{-j\psi n} \tag{4.1}$ 令$z=Ae^{j\psi}$，得到 $X(z)=\sum_{-\infty}^{\infty}x[n]z^{-n} \tag{4.2}$ 与z变换公式相同，由此可知傅里叶变换就是傅里叶变换的离散形式。

用法及意义

​ 傅里叶分析包含傅里叶级数与傅里叶变换。傅里叶级数用于对周期信号转换，傅里叶变换用于对非周期信号转换。但是对于不收敛信号，傅里叶变换无能为力，只能借助拉普拉斯变换。（主要用于计算微分方程）。而z变换则可以算作离散的拉普拉斯变换。（主要用于计算差分方程）从复平面来说，傅里叶分析只注意虚数部分，拉普拉斯变换则关注全部复平面，而z变换则是将拉普拉斯的复平面投影到z平面，将虚轴变为一个圆环。

​ 三种变换由于可以将微分方程或者差分方程转化为多项式方程，所以大大降低了微分（差分）方程的计算成本。

小波变换

从时域到频域,频域的时间信息消失了,你有没觉得之前我们分析的信号都太理想化了,现实中的信号往往随着时间而变化并非一成不变的,比如一辆车向你开来然后远去,你会听到声音从尖锐逐渐变得浑浊,这是多普勒效应造成的,而你收到的声音信号也由高频逐渐变为低频,而傅里叶变换只能告诉你信号中存在某种频率的信号,但却不能告诉你这个频率的信号是在什么时候出现的.它可能一直存在,或者只存在前半段信号里,可能存在后半段信号里.或者别的区间.

这个时候,又出现了傅里叶变换的改进版本,叫短时傅里叶变换.简单来说就是一段信号,假如这个信号长度是1秒,那么就每隔0.1秒就做一次傅里叶变换,总共做10次,这样,第一个变换的结果对应0-0.1s的信号频谱,第二个变换结果对应0.1-0.2s的信号频谱。

虽然短时傅里叶提供了一个粗糙版本的方案把时间的概念引入频域,但无法解决信号拟合的问题,我们使用正弦波去拟合方波,我们就需要用无穷多个不同频率的正弦波去拟合以抵消时频间的能量差异,简单来说,一个方波我们用正弦波去拟合,最终会拟合成这个样子。

为了解决上面两个问题,小波变换诞生了,要使用小波变换,在进行变换前首先需要挑选合适的母小波(也常常叫基波函数,以前实验室里经常被用来调侃:喲,你搞个基波啊),然后通过对母小波的平移和缩放,最终去拟合原信号,在平移的过程中,最终也把时间信息带入了频域(小波域)中,同时不同的母小波也更好解决了信号的拟合问题,当然,大多小波变换的核心原理,最终和傅里叶变换一样,利用了正交性来检波(有的基波没有正交性,例如morlet和mexican hat,这类小波在用于离散小波变换时有限制性)

那么如何挑选母小波呢?不用担心,数学大佬们为我们总结了一堆好用的母小波,按照响应的情况挑选就行了

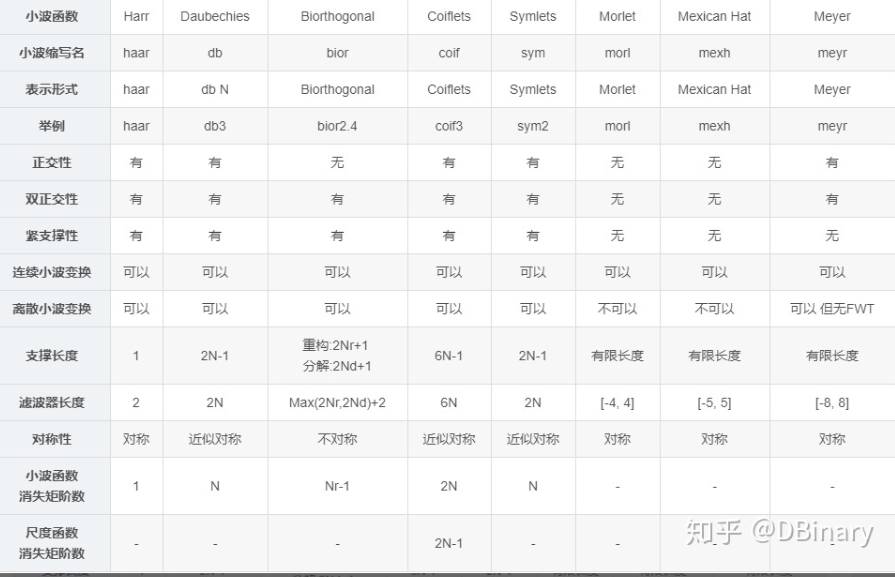
参照链接

作者：DBinary链接：https://www.zhihu.com/question/22085329/answer/774074211

---

• Previous
  电脑重装
• Next
  希尔伯特变换

---